Hong

Random and Fair Red Pockets: A Statistical Approach

Introduction

In many Asian cultures, it’s customary to give red pockets filled with money to children and loved ones during special occasions like weddings and holidays. But have you ever wondered how to divide the money fairly and randomly among the red pockets? In this note, we’ll explore statistical approaches to solve this problem.

The Problem

We want to divide a sum of money (without loss of generality, we assume the sum of money is 1) into N red pockets, ensuring each pocket has an equal chance of receiving a certain amount. However, we don’t want to divide the money strictly evenly, as that would make it less exciting. Our goal is to find a method that balances fairness and randomness.

Why Uniform and Normal Distributions Won’t Work

At first glance, sampling from a uniform or normal distribution might seem like a straightforward solution. Unfortunately, neither of them would generate samples meet the fairness requirements - which is, money amounts in all pockets shall follow an identical distribution.

Normal distribution is the maximal entropy distribution with fixed mean and variance. Because it’s domain is not bounded on the negative side, its sample can potentially be negative, thus will not fit the needs of money allocation.

Uniform distribution is the maximal entropy distribution for a given support. While we can bound its support to non-negative values, and constrain its mean to 1/N, we still can not take N samples from that distribution. Because we want all samples sum up to 1, which leaves us about N-1 degrees of freedmen. After you sampling N - 1 variables, the last one have to be obtained by $1 - \sum{x_i}$, which will pose a different distribution than the first N - 1 samples.

Random String-Cutting Problem

Let’s step back and reformulate it into a random string-cutting problem. Intuitively, randomly split money into N red pockets is equivariant to randomly cutting a fixed length string into N pieces. The sampling process, in this way, is converted from sampling N random amounts money with respect to a fixed total, into sampling (N - 1) cutting points.

import numpy as np

def cut_string(total_amount, num_pockets):
    # Generate N-1 random cutting points
    cutting_points = np.random.uniform(0, total_amount, num_pockets - 1)
    cutting_points = np.sort(cutting_points)

    # Calculate segment lengths
    segment_lengths = np.diff(np.concatenate([[0], cutting_points, [total_amount]]))

    return segment_lengths

# Example usage
total_amount = 100
num_pockets = 5
print(cut_string(total_amount, num_pockets))

Because the cutting point sampling is not constrained by the total sum value, cutting string can be performed as (N - 1) independent Uniform(0, 1) sampling.

Let’s also quickly verify the fairness of this approach - that is, each segment of string after cutting would have the identical length distribution.

Based on the order statistic, the PDF of the k^th segment length t_k from uniformly cutting an unity length string is

\[\begin{align} f(t, k) = \binom {n} {k} k (n - k) \int_{x = 0}^{1-t} x^k (1 - x - t)^{n - k - 1} dx \end{align}\]

by applying integration by parts rules once, we get

\[\begin{align} f(t, k) & = 0 + \binom {n} {k+1} (k + 1) (n - k - 1) \int_{x = 0}^{1-t} x^(k+1) (1 - x - t)^{n - k - 2} dx \\ & = f(t, k+1) \end{align}\]

Thus we get the equivalence of the density functions for all divided segment lengths, which indicates a fair splitting process. Actually this sampling approach is not only going to give you a fair but also a maximum entropy distribution for each divided segments, which is, with minimum assumptions on the shapes of the segment length distribution.

Normalized IID Sampling

Let’s step back to the original problem. If the only goal is to sample N amounts of money with a fixed total amount and an identical distribution for each sampled amount, we can simply perform N IID sampling from a distribution H(x) and apply a normalization to make N samples sum to 1.

There is no other requirements on the H(x) distribution type, other than its support need to be non-negative.

import numpy as np

def normalized_sampling(total_amount, num_pockets):
    # Use Uniform[0, 1] to perform sampling, but can replace it with any other non-negative distributions
    sampled_amount = np.random.uniform(0, 1, num_pockets)
    normalized_amount = sampled_amount / sampled_amount.sum()
    return normalized_amount

# Example usage
total_amount = 100
num_pockets = 5
print(normalized_sampling(total_amount, num_pockets))

You may be wondering, how would this simple approach different from the uniform string cutting approach mentioned above, and how would different distribution it samples from affect the final red pockets money distribution ?

You may already realize that, even though both approaches can generate “fair” sampled results, in respect to the “identical distribution”, but the final sampled money distribution generated from the second approach is not necessary maximal entropy, like the first one does. It means that it may apply additional assumptions (information) to the sampled money amount. Then what are those assumptions ?

Control the “Randomness”

In the above explanations, we only talked about the “fairness” of the sampling process, but leave the randomness unspecified. The how do we define the “randomness” in this process ?

Let’s imagine some extreme cases - If we split the money evenly into N pieces, each piece then become a fixed amount. It is still fair, but completely without randomness. On the other hand, if we use the second approach to sample from a 2-hots distribution with either 0 or 1, the money amounts would vary a lot.

We can then define the variance of the splitted amounts as the randomness of the splitting process. The lower variance means the splitted amounts more concentrated to their mean (1 / N), and higher variance means otherwise.

With the above definition and some stats calculations, we can derive the randomness of the final money splitting by using the second approach, which is proportional to the mean and variance of the sampling distribution H(x). In particular, we have

\[Randomness \propto \frac{\sigma_{H(x)}^2}{\mu_{H(x)}^2}\]

By controlling the sampling distribution mean and variance, we can get different level of randomness during money splitting.

Create Red-Pockets with Different Weights

To generalize this problem further, if we do not want to always split the red pockets evenly, let’s say, we want give more money to some kids than others, how can we still accurately control the randomness and the money splitting ratios ?

The generalized splitting distribution actually maps to a well known multi-variants distribution - Dirichlet distribution.

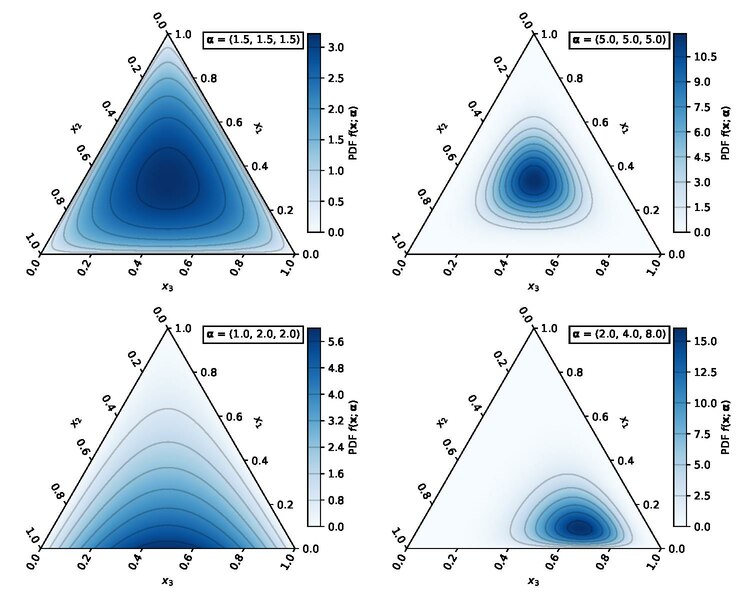
As you can see from the above Wiki figure, sampling from this distribution would happens on a N - 1 simplex. You can assign different Dirichlet parameters to control the different weights for each red pocket and the randomness of the splitting (the concentration or variance of the distribution).

When we set all the weights to 1, it becomes flat Dirichlet distribution, and sampling from it is exactly same as sampling from our first approach.

import numpy as np
from scipy.stats import dirichlet

def dirichlet_distribution(total_amount, num_pockets, weights=None):
    if weights is None:
        weights = np.ones(num_pockets)

    # Sample from Dirichlet distribution
    sample = dirichlet.rvs(weights)

    # Scale sample to total amount
    scaled_sample = sample * total_amount

    return scaled_sample

# Example usage
total_amount = 100
num_pockets = 5
weights = [1, 2, 3, 4, 5]  # Optional weights
print(dirichlet_distribution(total_amount, num_pockets, weights))

The sample code I shared above demonstrated how to use built-in Dirichlet random generator to perform the sampling. If you are interested in how to perform Dirichlet sampling on your own, please follow my Dirichlet Sampling Notebook for more details.

Conclusion

In this note, we shared 3 different statistical approaches to split the red pockets money. We analyzed their different characteristics and demonstrated the sampling process in python code.

If you are interested in reading more stats cookies like this, please comment in the post.