分期付款和e 的故事

程序员多年，你是否还记的当年大学里伴随自己多年的e ? 没错，就是科学计算中的那个无理数

哦，什么，你在买房计算贷款的时候还看见过它？嗯，不错，就是在计算利息的时候。

比如今年，小明同学贷款1000k 买了套房，如果年利率是6%，假设小明在中途没有还款，请问贷款10个月时间小明需要支付的利息由多少？

这太简单了，10个月时间也就是是1年的5/6 ， 那么其利率就是年利率的5/6，也就是5%。 利息是50K。计算非常正确，可是在实际生活中，资本家们是不会这么计算利息的。

“但是，明明年利率是6% 呀”，也许你还不服气，问题在哪儿呢？聪明的你必然已经想到，银行买房贷款（或者信用卡贷款）的利息结算一般并非按照年为单位，并平摊到每个月；而是会把利息是按照月来结算，如果每个月你没有把你所欠的利息还清的话，那些利息就会自动滚入本金，在下个月中计算复利，也就是传说中的利滚利。

现在我们再来看一下，按照复利来计算，小明将要支付多少利息:

每个月本金加利息的总额变化率为 ，其中 r 表示年利率。那么n 个月后本金加利息总额变化是 ，所以在本例中，10月后小明的利息和本金总额是 ,也就是说其利息总额为 比预期的50K多付了1千多美元。

如果你认为银行的利息计算非常黑的话，那么就请记的按时每月还款哦。

接下来，让我们再来脑洞大开一下：如果银行不是按照每月来结算利息，而是按照天来计算复利呢？直觉告诉我们，我们会被银行压榨的非常多。那到底是多少呢，让我们来计算一下：一年共有365 天，而10 个月也就是304天，代入上面的公式我们本息总额有

小明总共需要支付的利息为，看起来似乎只是比按月结算多了一点点：不到100刀。

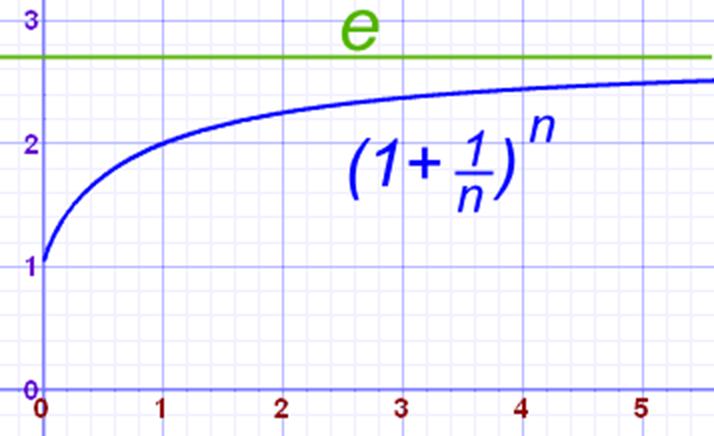
这么算来，看似疯狂的复利计算，似乎还不会随着其结算时间划分的不断增加而无限增长。

那么问题来了，在极端情况下，也就是银行利息结算划分数达到无穷大的时候，小明的利息会无限增加吗？如果不是，那么其极限又是多少呢？根据之前的计算，我们知道，当把一年划分n 份的时候，小明的10个月中约占有份。那么，之前的公式变成了如下

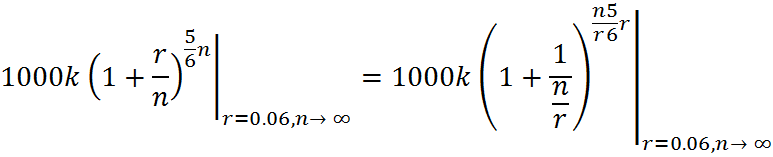
我们对变量进行替换，令, 使得原式

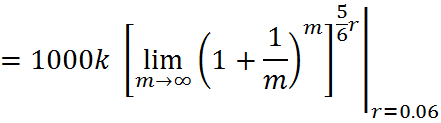
原式是否收敛，就是决定于这个极限是否是收敛的。幸运的是，这个极限的确是收敛的，而且它的收敛值就是我们之前提到的，你大学中学到的一个常量，。

那么上式就变成了 ，总共多付利息1.27k。

其实这个通过资本复利计算得到的一个上限值，也就是我们通常对货币计算未来/过去价值时使用的一个公式，它表示了极端情况下固定回报率的投资最大回报。

也就是说，当固定的单位利率为r ，那么在n个单位时间的未来，当前价值x 的资本在那个时候价值变成了

好了，今天的故事就讲到这里。也许作为一个程序员的你早就熟谙了这些基本的金融常识，不过既然你已经看到这里了，就顺便分享一下吧J。