闲谈生成模型和判别模型

最近有很多同学向包子君提问关于生成模型和判别模型的区别和共同点，于是包子君决定跟大家分享一些这方面的心得。

我们首先来看两个我们常见的分类模型。不失一般地，我们采样y 来表示标签变量，使用 来表示 feature 向量。当我们假设在标签已知的时候（如下图所示），所以的分类feature 都相互独立时，我们便可以建立naïve 贝叶斯模型来对feature向量进行分类。

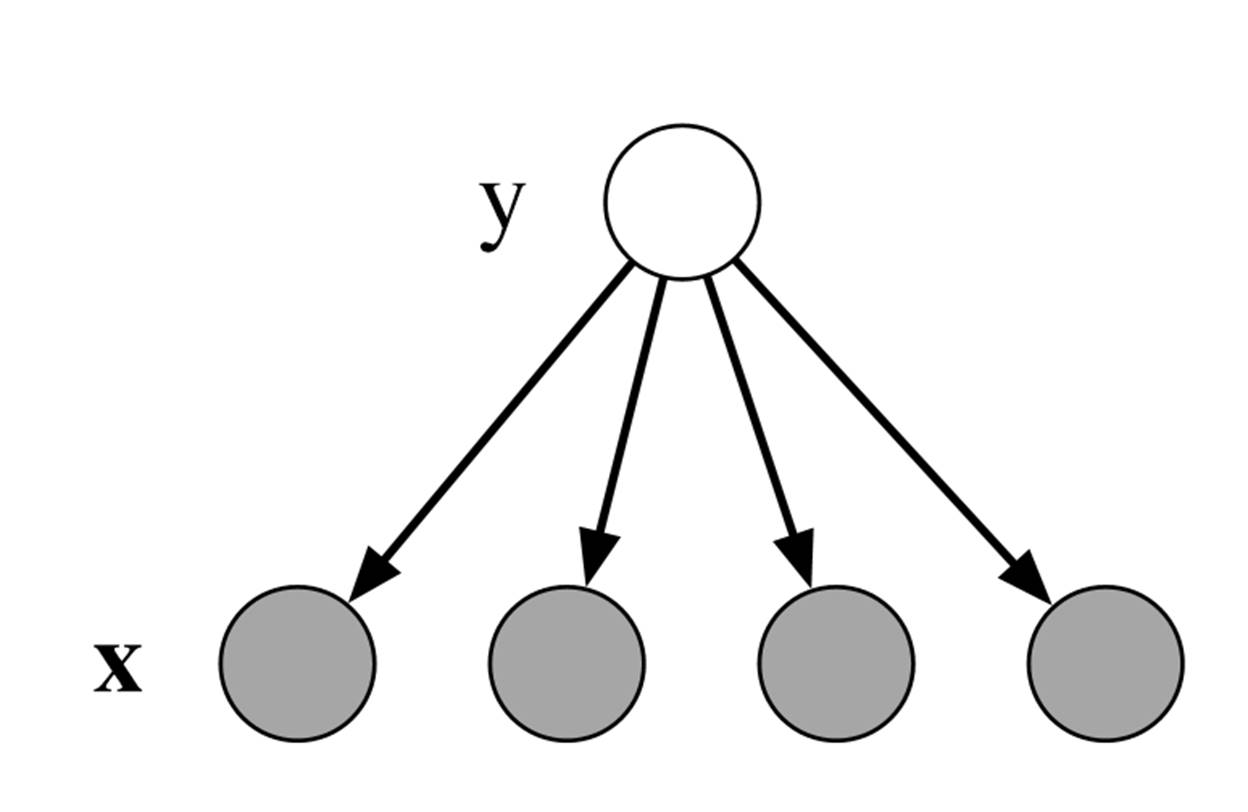
Naïve 贝叶斯分类是根据如下联合概率分布来得到标签和模型的关系的：

另外一种常见的分类方法就是logistic regression 。这种分类方法是以假设对于每个类别y， 是由关于 的线性分布以及一个归一化常量决定的。表达式如下

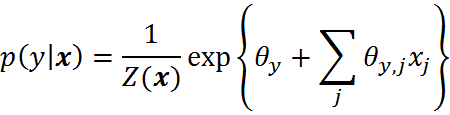
其中， 是一个归一化常量。

上述这两个模型，虽说都是描述 分布的，但是他们却有着不同的角度。对于像naïve 贝叶斯这样的典型的生成模型而言，它们是由 这样的联合概率分布分解得到的，他们详细描述了如何通过标签y 来生成feature 向量 x 。而对于一个判别模型来说，比如 logistic regression，是由一类如 这样的条件概率分布模型组成的。换个角度来说，这种模型直接模拟了分类器所需要的概率分布。理论上来说，我们也可以给判别模型加上一个关于x 的概率函数 来得到 这般的概率分布，但实际中很少会需要这么做。

根据上述分析，我们可以清楚地看到，判别模型的根本概率公式中缺少一个先验概率 。而正恰恰是这个先验概率，往往在实际中是很难得到的，因为feature 之间互相独立的情况在实际中少之又少。举一个例子来说，我们常常使用 HHM （生成）模型来建模自然语言处理中的名字提取。如果每个单词的标签（代表是否是名字）只仅仅依靠于当前单词这一个 feature ，那么整个识别率会相当低。实际中，我们会引入更多的比如单词是否首字母大写，后缀，它的其它相邻单词是什么等等前后相关的复杂且互相依赖的feature列表。

所以相对于生成模型，判别模型主要的优势就是可以无视复杂且相互依赖的feature 向量是如何分布的，从而大大地简化了模型的训练和使用。但是这并不是说生成模型就一无是处了，相反的，在有些情况下生成模型有它独特的优势。比如在很多隐藏变量且标签不完整的时候，有一个完整的生成模型可以更有效地进行非监督学习；而当训练数据非常少的时候，p(x) 先验概率的平滑效果也可以帮助训练的效果。