完美的硬币 (一)

问题的引入：

假如有人给你一枚材料未知的硬币，请问你要如何做才能确定当这枚硬币被抛起落地时，其正反面向上的概率相等，也就是说，这是一枚完美的硬币。

这是一个看似简单的问题，包子君相信同学们心里一定已经在默默地回答了：反复抛这枚硬币呗，如果是完美的硬币，那么其落地时正面向上的次数和反面向上的次数应该差不多相等。

没错，我们的直觉和经验就是这么告诉我们的。但是大家有没有想过，其实上面的说法有几个漏洞：

1. 学过概率论的同学一定知道，频数和概率是不一样的。此问题问的是硬币的概率是否正反面相等，而你的实验统计的是频数。通过频数推导概率有一个置信度的问题。

2. 试验中硬币正面向上和反面向上的次数差不多是多差不多？相差1次，2次还是10次，100次?

假设分析：

First thing first, 为了证明硬币的完美性，按照数据分析的老规矩，我们首先得给出两个假设。为了方便起见，我们设定我们的 Ground Truth (null假设) 是我们的硬币是完美的，与之对应的 (alternative 假设) 便是硬币是不完美的。默认情况下，我们认为Ground Truth 是成立的，只有我们的数据满足一定的边界条件，使得Ground Truth 条件成立的P-Value 小于5% 时，我们认为Ground Truth 被打破，其对应的假设成立。在这里，P-Value 指的是当Ground Truth 成立时，当前事件发生的概率有多大。

贝叶斯估计：

我们知道，对于投掷硬币来说，如果是同一颗硬币（其正面向上的概率已经给定），那么掷硬币试验得到的正面向上的频数是符合二项分布的。对于一个正面向上概率为p的硬币来说，总共抛硬币n 次，x 次向上的事件发生的概率为：

那么，假设硬币正面向上的先验概率是均匀分布的，我们从抛n次试验观察到x次正面向上可以得出硬币正面向上的后验概率是：

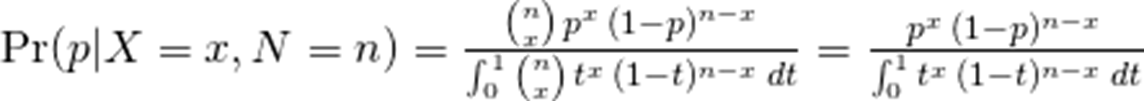
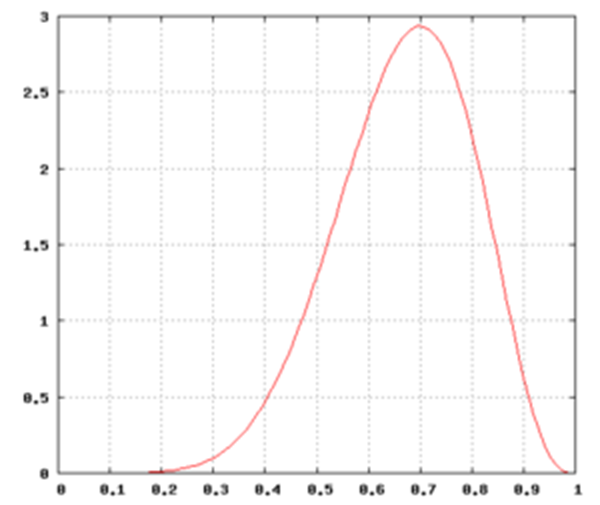
我们可以将分母看成是一个由X,N 决定的normalization常数C(x, n)，那么，硬币正面向上概率的概率分布曲线则又是一个类似于二项分布的密度曲线(下图为当 n = 10, x = 7 时的曲线)。

当p = x / n 时，其概率函数Pr (p|X=x, N=n) 取得最大值，这也是通过观察对硬币正面向上概率p 的最佳估计（最大后验估计）。

假设论证：

回到我们最初的假设上面。我们现在需要对最开始的Ground Truth 进行一个量化。我们将完美的硬币定义成其正面向上的概率为 P = 0.5。但是我们知道，由于P 是一个连续的变量，我们必须定义其一个容忍（误差）范围，才能使得估计有意义。于是我们可以假设误差范围是0.05, 也就是当 ，我们的Ground Truth 成立。

我们将P 的概率范围带入上节中的后验概率密度函数，得到Ground Truth 成立的概率是：

根据我们之前定下的P-Value, 只有当以上积分函数的值小于 0.05 时，我们的Ground Truth才被推翻，而与之对立的 alternative假设被认为正确；反之，我们默认认为还没有足够的数据来证明我们的Ground Truth 假设是错误的。

在这里，包子君给没有学过统计的同学们再次强调下，我们之前的两个假设 Ground Truth 和 alternative 假设并非是完全平等的；相反的，我们往往会更偏向于Ground Truth 假设，只有当其alternative 假设的置信度超过一个很大的值时，才承认其正确性。所以，在使用统计证明某个观点时，我们往往会先假设其反面的 null 假设作为 Ground Truth, 而把观点本身作为alternative 假设。在证明时通过推翻 null 假设来达到正面当前观点的目的。