深入浅出采样估计

在之前的文章里，我们通过贝叶斯的方法来解答了“硬币是否均匀”的问题。在那个问题里，我们首先提出了“硬币是均匀的”的假设，然后使用贝叶斯理论得到后验概率Pr (硬币是均匀的|观察N次抛硬币) , 并且根据后验概率来得出最终的结论。使用这种方法，我们的确可以有效地验证一个假设，但是却不能靠它来系统地直接对一般的采样问题（sample）进行估计。举个例子来说，如果给你一个硬币，在不知道它是否是fair 与否的情况下，我们如何来设计实验，从而直接得到一个估计的概率值——硬币正面向上的概率是多少。

直觉上来看，有同学可能会认为上面这个问题的答案其实很简单，就是通过反复地投掷硬币，并统计求出其正面，反面向上的总次数。通过 正面向上次数/总共投掷次数 即可得到此硬币正面向上的概率。

但是仔细想想，上面的估计还是有些问题的。比如说，为什么我们通过投掷硬币得到正反面次数就可以得出硬币本身的bias ? 通过投掷实验对硬币的估计的准确性又有多少？如果你还是没想明白问题在哪里的话，可以考虑下这个问题：如果你只投掷两次硬币，且结果全部为向上，你能就认定这个硬币投后得到正面向上的概率是100% 吗？如果不能，那又需要投掷多少次硬币才能确定呢？

其实这是一个很基本的采样估计问题，几乎在任何科学实验中都会首先被问到。让我们用数学模型来表达下以上问题。我们可以把当前硬币投掷后得到的正反面看成是一个 0 – 1 随机变量。每一次掷硬币时看成是对这个随机变量经行一次独立同分布的采样。我们所要求得是这个随机变量分布中值为1时（正面向上）的概率（也就是这个随机分布的一个参数）。这种随机分布的参数是非常常见的，我们称之为 population proportion，我们一般记作 p。于此对应的常见的参数还有population mean （平均值），以及 population variance (方差)。

而我们设计实验，就是设计对此随机变量进行采样方法和次数，来估计随机分布的参数（population proportion）。

在我们的试验中，对随机变量经行n次采样后，我们可以对我们的样本随机变量进行一个值为1次数的统计，除以总数后得到一个对于样本的sample proportion 的统计，我们记为。

根据大数定理，我们可以得到，当采样数据足够多的时候，对随机变量population proportion 的最佳点估计就是sample proportion。具体的公式如下：

这么看来，我们之前用多次抛硬币来估计硬币正面向上发生的概率还有几分道理。可是，这个问题并没有被完全的解决。虽然大数定理可以说明在样本不断变大的时候，我们用采样均值来估计随机变量分布的概率会越来越准确。可是对于一次具体的估算来说，到底要采样多少次，也就是要扔多少次硬币才能说明足够准确呢？

这个问题实际上就是在考量用样本估计概率分布的时候的误差问题。我们假设定义这个误差是ɛ, 那么我们可以有如下表达：

而著名的中心极限定理，就是给出了这个ɛ 的分布。

通过中心极限定理，我们可以知道，当样本数目足够多的时候，ɛ 的分布是一个正太分布。表达式如下：

在此算是中指的是我们假设的这个随机变量的方差（注意，不是我们样本的方差），而n 则指的是我们采样的数量。我们可以感觉到，通过采样（抛硬币实验）的方法来估计概率分布（硬币向上的概率），估计的准确性同时取决于我们采样的数量，以及这个随机变量本身的不确定性。下图很好地表达了p, , 以及ɛ 之间的关系。

当我们的样本数量增加时，我们通过来对p进行估计的误差方差就会降低，整个正太分布的形状也会更加尖锐一些，如下图所示：

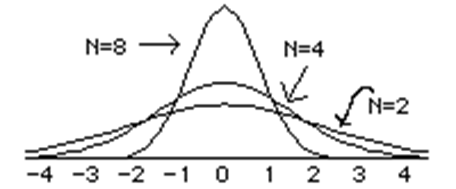
所以，样本数量，随机变量本身的方差大小，以及 p 和 组成了一个相互关联的整体。下面我们就来说说他们之间的关联对采样估计来说有什么深刻的意义。

我们首先来引入一个统计中常用到的概念：置信度。置信度表示的是你的统计估计和实际事实之间的吻合程度，它是判断你估计准确性的重要指标。

对于估计好坏来说还有另外一个指标就是叫做精度。估计的精度便指的是估计中所能容忍的系统误差是多少。举个例子，如果一个概率估计的精度是，那么凡是落在这个区间内的所有概率都属于被正确估计了。

估计的置信度和精度往往是一对相互拮抗的概念。外部条件不变的情况下，置信度高了往往精度就下降了，反之亦然。举一个简单的生活中的例子：比如你要测量头发的粗细，如果你声明你的测量精度是厘米级别的，那么你很容易得到“总是正确”的结果；但要是你声明你的精度是微米级别的，在测量工具不变的情况下，那么即使你再怎么小心，你测量的可信度都不会太高。

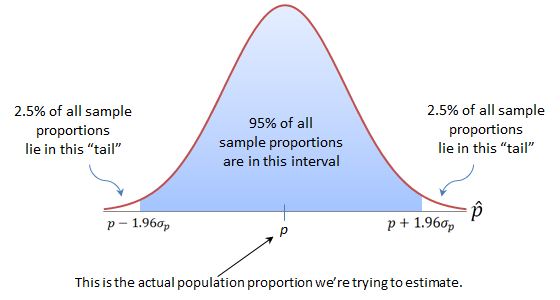
回到我们讨论的主题上来，当我们对随机变量的population proportion 进行估计的时候，首先需要确定的便是我们需要怎样的置信度。通常情况下我们要求估计的置信度达到95%，也就是常说的95T。95%的置信度表示在p 相对于 的分布上，可容忍误差需要cover如下图所示的一段区间。

这段正太分布上的区间通过变换可以换算到相对于p值得一个确切的值，也就是所能够达到的精度。具体公式如下所示：

在这里指的是原随机变量的标准差。我们知道我们假设的随机变量（抛硬币的结果）服从伯努利分布，那么上式就可改写成

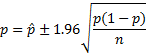
为了能够估算上式，我们用的最佳估计来取代其值，也就得到了我们最终精度表达式：

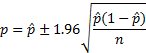
接下来需要做的事情，就是根据我们对精度的要求来确定采样的数目，也就是n 的大小。比如，当我们需要误差不超过3% 时，我们的抛硬币次数需要为:

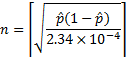
至此，包子君带领同学们科学，系统地对硬币的均匀性进行了一次估算，希望对大家在数据科学面试中能有所帮助。